Las leyes de Kepler describen la cinemática del movimiento de los planetas en torno al Sol.
Primera ley
Los planetas describen órbitas elípticas estando el Sol en uno de sus focos
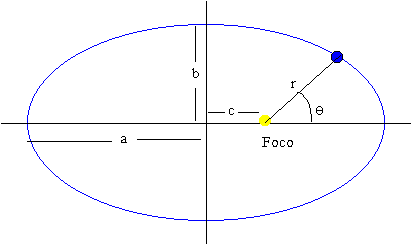
Una elipse es una figura geométrica que tiene las siguientes características:
- Semieje mayor a
- Semieje menor b
- Semidistancia focal c
- La relación entre los semiejes es a2=b2+c2
- La excentricidad se define como el cociente e=c/a
- r1 es la distancia más cercana al foco (cuando q=0) y r2 es la distancia más alejada del foco (cuando q=p). Vemos en la figura que r2+r1=2a, y que r2-r1=2c
Segunda ley
El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.
La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular es el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol.
(Es necesario disponer de un explorador compatible con JDK 1.1. para ejecutar el subprograma).
Tercera ley
Los cuadrados de los periodos de revolución son proporcionales a los cubos de los semiejes mayores de la elipse.
(Es necesario disponer de un explorador compatible con JDK 1.1. para ejecutar el subprograma).
Como podemos apreciar, el periodo de los planetas depende solamente del eje mayor de la elipse. Los tres planetas de la animación tienen el mismo eje mayor 2 a=6 unidades, por tanto, tienen el mismo periodo.
